فروض کلاسیک در ایویوز

فروض کلاسیک رگرسیون به مجموعه‌ای از پیش‌فرض‌ها اشاره دارد که برای اعتبار و دقت نتایج به دست آمده از مدل‌های رگرسیونی لازم هستند. فروض کلاسیک در ایویوز، شامل خطی بودن، استقلال، همسانی واریانس (هترو اسکداستیستیسی)، نرمال بودن خطاها و عدم هم‌خطی چندگانه می‌باشد.

رعایت این فروض به تحلیل‌گران کمک می‌کند تا از اعتبار نتایج و پیش‌بینی‌های به دست آمده اطمینان حاصل کنند. به طور خاص، فرض نرمال بودن خطاها و همسانی واریانس اهمیت ویژه‌ای دارد، زیرا نقض این فروض می‌تواند به نتیجه‌گیری‌های نادرست و بایاس در تخمین‌ها منجر شود. برای برقراری ارتباط با گروه داده پردازی ایران آمار از طریق لینک‌های زیر اقدام نمایید.

بررسی فروض کلاسیک در ایویوز

درآموزش قبل مفهوم فروض کلاسیک رگرسیون بررسی شده است و در این آموزش از فروض کلاسیک در نرم افزار ایویوز آزمون‌های فرض‌های میانگین جملات خطا (باقی مانده‌های مدل) برابر صفر، ناهمسانی واریانس جملات خطا (باقی مانده‌های مدل)، عدم خود همبستگی بین جملات خطا و نرمال بودن توزیع باقی مانده‌ها بررسی شده و در صورت پذیرفته نشدن فروض راه حلی برای اختلال مربوطه بیان شده است.

اهمیت رعایت فروض کلاسیک در تحلیل‌های ایویوز

رعایت فروض کلاسیک در تحلیل‌های ایویوز به عنوان یک اصل بنیادی برای حصول اطمینان از اعتبار و دقت نتایج مدل‌های رگرسیونی شناخته می‌شود. عدم رعایت این فروض می‌تواند به نتایج نادرست و غیرقابل اعتماد منجر شود. به عنوان مثال، اگر فرض همسانی واریانس نقض شود، تخمین‌های مربوط به ضرایب ممکن است ناپایدار و غیرقابل اعتماد باشند، که در نهایت به خطاهای تحلیلی و تصمیم‌گیری‌های نادرست منجر می‌شود.

علاوه بر این، بررسی و رعایت فروض کلاسیک به تحلیلگران کمک می‌کند تا نقاط ضعف و نارسایی‌های ممکن در داده‌های خود را شناسایی کنند. با استفاده از ابزارهای آماری موجود در ایویوز، می‌توان به راحتی این فروض را آزمایش کرد و در صورت نیاز، اقدامات اصلاحی انجام داد. این امر نه تنها کیفیت نتایج را افزایش می‌دهد بلکه به اعتبار علمی پژوهش‌ها نیز می‌افزاید. در نهایت، پایبندی به فروض کلاسیک نه تنها به بهبود دقت تحلیل‌ها کمک می‌کند، بلکه به ایجاد اعتماد در نتایج ارائه شده نیز می‌انجامد، که این موضوع در زمینه‌های تحقیقاتی و صنعتی از اهمیت بالایی برخوردار است.

صفر بودن میانگین خطاها فروض کلاسیک در ایویوز

بعد از وارد کردن داده ها در ایویوز و برآورد مدل رگرسیونی در ایویوز،نرم افزار مقادیر باقی مانده‌ها را در سری با نام resid در صفحه‌ی کاری (workfile) ذخیره می‌کند. نکته‌ی مهم این است که با هر تغییر در مدل، مقادیر این پوشه توسط نرم‌افزار ایویوز به روزسانی خواهد شد. پس ابتدا پوشه‌ای (سری‌ای) در نرم‌افزار ذخیره باید کرد تا مقادیر اولیه باقی‌مانده‌ی مدل در آن ذخیره شود. برای این منظور در محیط تخمین مدل مانند تصویر از آدرس Proc/Make Residual Series  دکمه Ok را باید زد. با این کار پوشه‌ی جملات خطا مدل در صفحه‌ی کاری با نام resid01 ذخیره خواهد شد.

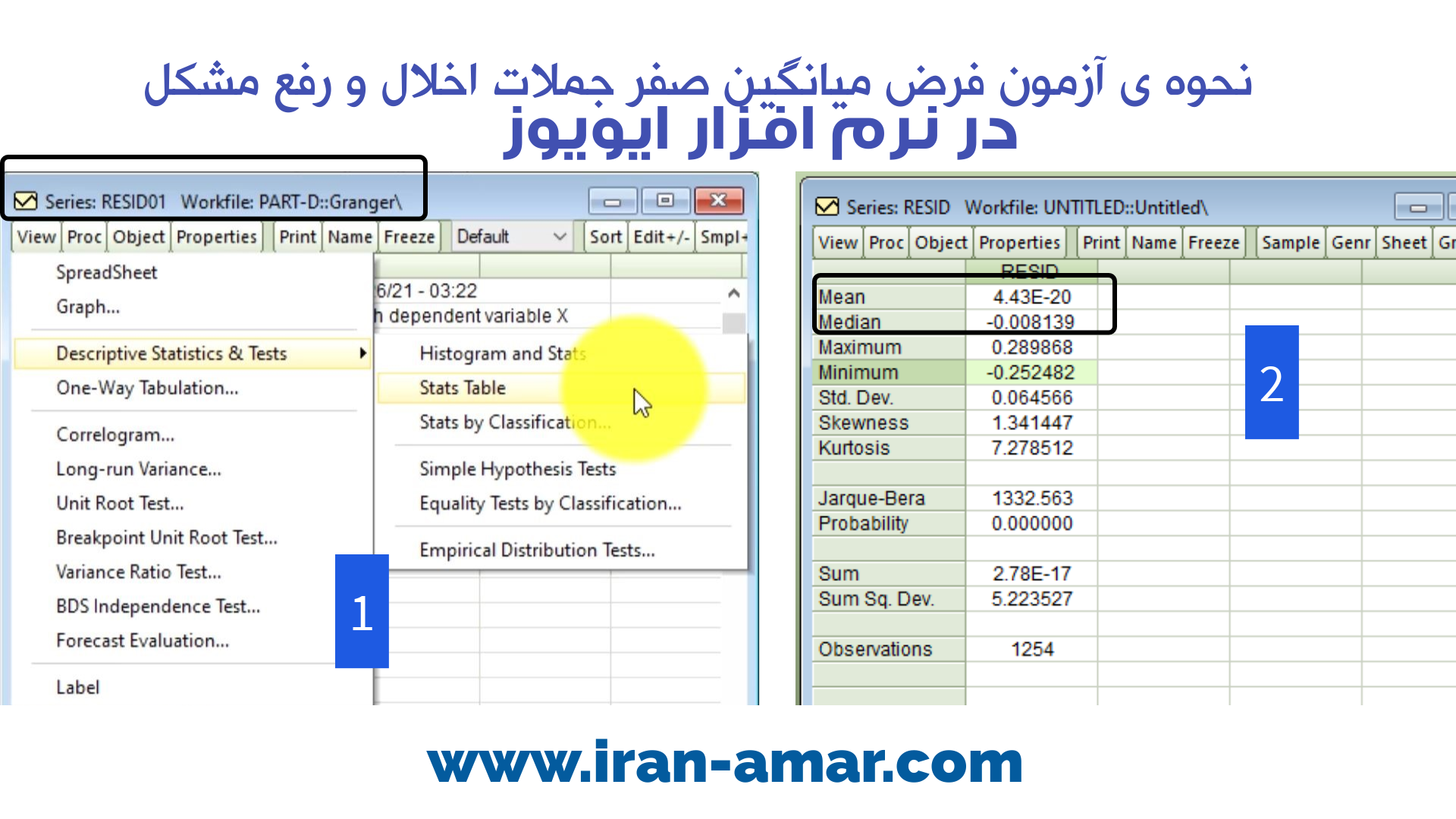
برای بدست آوردن میانگین جملات خطا (اخلال) چند راه در نرم افزار ایویوز وجود دارد که یکی از روش‌ها در ادامه بیان شده است. بعد از ذخیره‌سازی پوشه‌ی باقی‌مانده‌ها،پوشه resid01 را باز کرده از تب View گزینه‌ی Descriptive Statistic & Test را انتخاب و گزینه State Table انتخاب شود. در جدول باز شده ستون اول و سطر اول مقدار میانگین جملات خطا نوشته شده است، این عدد معمولا نزدیک صفر است. در این مثال میانگین جملات خطا برابر عدد 4.4E-20 که بسیار نزدیک صفر است.

این آزمون همان‌طور که قبلا هم گفته شد در مدل‌های دارای عرض از مبدا برقرار است و نیازی به بررسی میانگین جملات خطا نیست. فرض بعدی از فروض کلاسیک در ایویوز ناهمسانی واریانس جملات اخلال است که در ادامه به بررسی آن پرداخته شده است.

آزمون ناهمسانی واریانس خطاها فروض کلاسیک در ایویوز

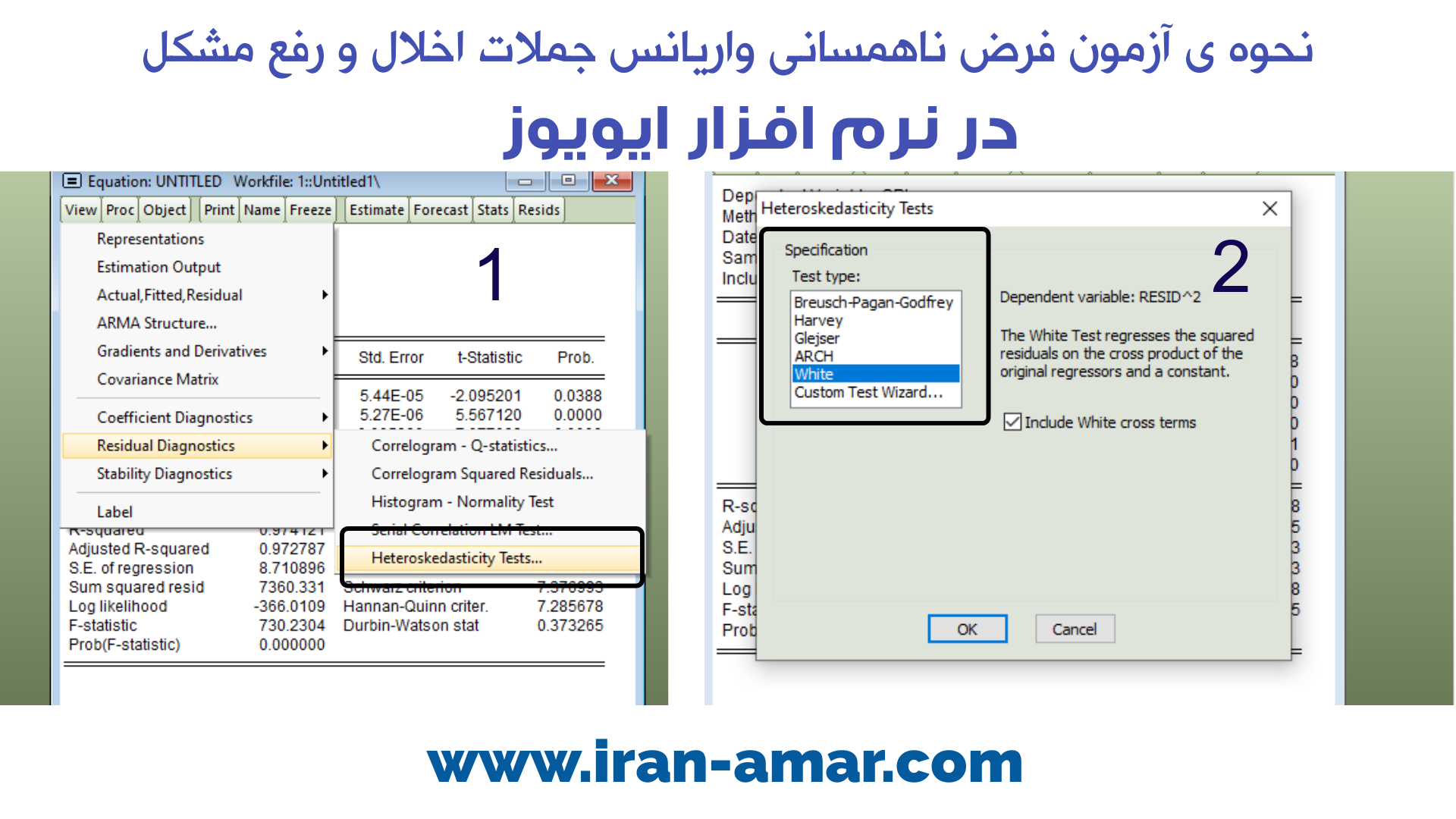
مفهوم ناهمسانی واریانس جملات خطا (اخلال) در آموزش قبلبیان شده است.(مفهوم فروض کلاسیک رگرسیون) برای بررسی ناهمسانی واریانس در جملات خطا (اخلال) مراحل زیر در نرم افزار ایویوز دنبای شود. پس از برآور مدل در نرم افزار ایویوز در محیط برآورد مدل از مسیر  View/Residual Diagnostics/Heteroskedasticity Test پنجره ای باز می‌شود. این پنجره با آزمون‌هایی برای تشخیص ناهمسانی مانند آزمون براش پاگان، آزمون وایت و … مدل را مورد بررسی قرار می‌دهد. دراین مدل از آزمون white استفاده شده است.

در آزمون وایت برای بررسی ناهمسانی واریانس خطاها از فروض کلاسیک در ایویوز پس از تخمین مدل رگرسیونی اولیه، با استفاده از مقادیر پیش‌بینی شده، خطاها محاسبه خواهد شد. سپس یک مدل جدید با مربع خطاها به عنوان متغیر وابسته و متغیرهای مستقل اولیه به عنوان متغیرهای مستقل قرار می‌گیرد. اگر فرض ثابت بودن واریانس خطاها نقض شود، این نشان‌دهنده وجود ناهمسانی واریانس است.

در ادامه پنجره ناهمسانی واریانس جملات اخلال آزمون شده و خروجی را نرم افزار نشان می‌دهد. احتمال آماره‌ی آزمون(Prob) اگر کمتر از 0.05 باشد،مشکل ناهمسانی واریانس خطاها از فروض کلاسیک در ایویوز وجود دارد.

رفع مشکل ناهمسانی واریانس فروض کلاسیک در ایویوز

برای رفع مشکل ناهمسانی واریانس فروض کلاسیک در ایویوز از تصحیح وایت استفاده شده است. تصحیح وایت با استاندار کردن انحراف‌معیار ضرایب سطح معناداری جدیدی برای ضرایب در مدل گزارش می‌دهد. برای انجام این کار در نرم افزار ایویوز در محیط برآورد شده‌ی  مدل از تب Estimate (1) تب Option (2) و در بخش Coefficient covariance matrixe گزینه‌ی HAC را انتخاب و در نهایت روی ok کلیک کنید.

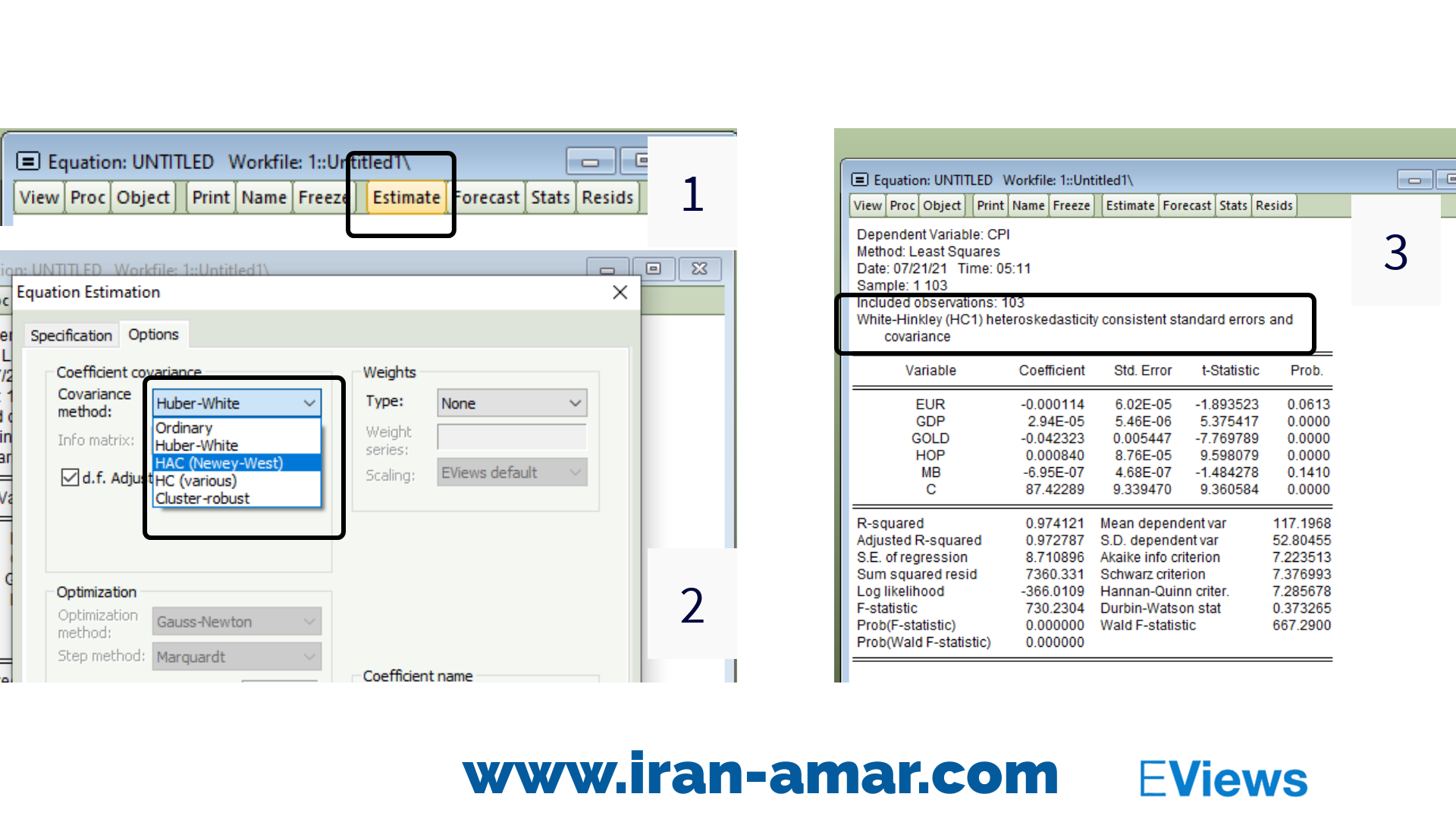
همانطور که تصویر بالا بخش 3 خروجی نرم افزار ایویوز نمایش داده شده است، مدل با برطرف کردن مشکل ناهمسانی از طریق روش HAC نتایج را گزارش داده است. تخمین‌گرهای HAC خطاهای استاندارد را به گونه‌ای اصلاح می‌کنند که تأثیر ناهمسانی واریانس و خودهمبستگی در داده‌ها را در نظر بگیرند. این بدین معناست که نتایج به دست آمده از آزمون‌ها و پیش‌بینی‌ها به طور قابل توجهی دقیق‌تر و معتبرتر خواهند بود. با استفاده از این تخمین‌گرها، بایاس ناشی از ناهمسانی واریانس کاهش می‌یابد. این به ویژه در تحلیل‌های اقتصادی و اجتماعی که داده‌ها ممکن است تحت تأثیر این مشکلات قرار داشته باشند، اهمیت دارد.

آزمون عدم خودهمبستگی خطاها فروض کلاسیک در ایویوز

برای پی‌بردن به این مسئله که باقی‌مانده‌ها دارای خودهمبستگی در مدل هستند درنرم افزار ایویوز چند راه وجود دارد. اولین راه توجه به آماره‌ی دوربین -واتسون خروجی مدل در نرم افزار است. آزمون دوربین-واتسون (Durbin-Watson Test) مناسب خودهمبستگی مرتبه‌ اول است. این آماره اگر مقدار بین 1.5 تا 2.5 داشته باشد مشکل خودهمبستگی بین جملات اخلال وجود ندارد.

آزمون دوربین-واتسون (Durbin-Watson Test) در دهه ۱۹۵۰ توسط جرج دوربین و ویلیام واتسون توسعه یافت. این آزمون به منظور بررسی خودهمبستگی در خطاهای مدل‌های رگرسیونی طراحی شده و به عنوان ابزاری کاربردی در تحلیل‌های آماری به سرعت مورد توجه قرار گرفت.

در سال ۱۹۵۰، دوربین و واتسون در مقاله‌ای به بررسی تأثیر خودهمبستگی بر تخمین‌های رگرسیونی پرداختند. این مقاله به طور خاص به روش‌های تخمین و تحلیل واریانس خطاها پرداخته و مفهوم خودهمبستگی را به شکلی جامع توضیح داد. به تدریج، آزمون دوربین-واتسون به یکی از ابزارهای اصلی در تحلیل رگرسیونی تبدیل شد. محققان و تحلیلگران داده‌ها از این آزمون برای شناسایی وجود خودهمبستگی در داده‌های سری زمانی و رگرسیون‌های پیچیده استفاده کردند.

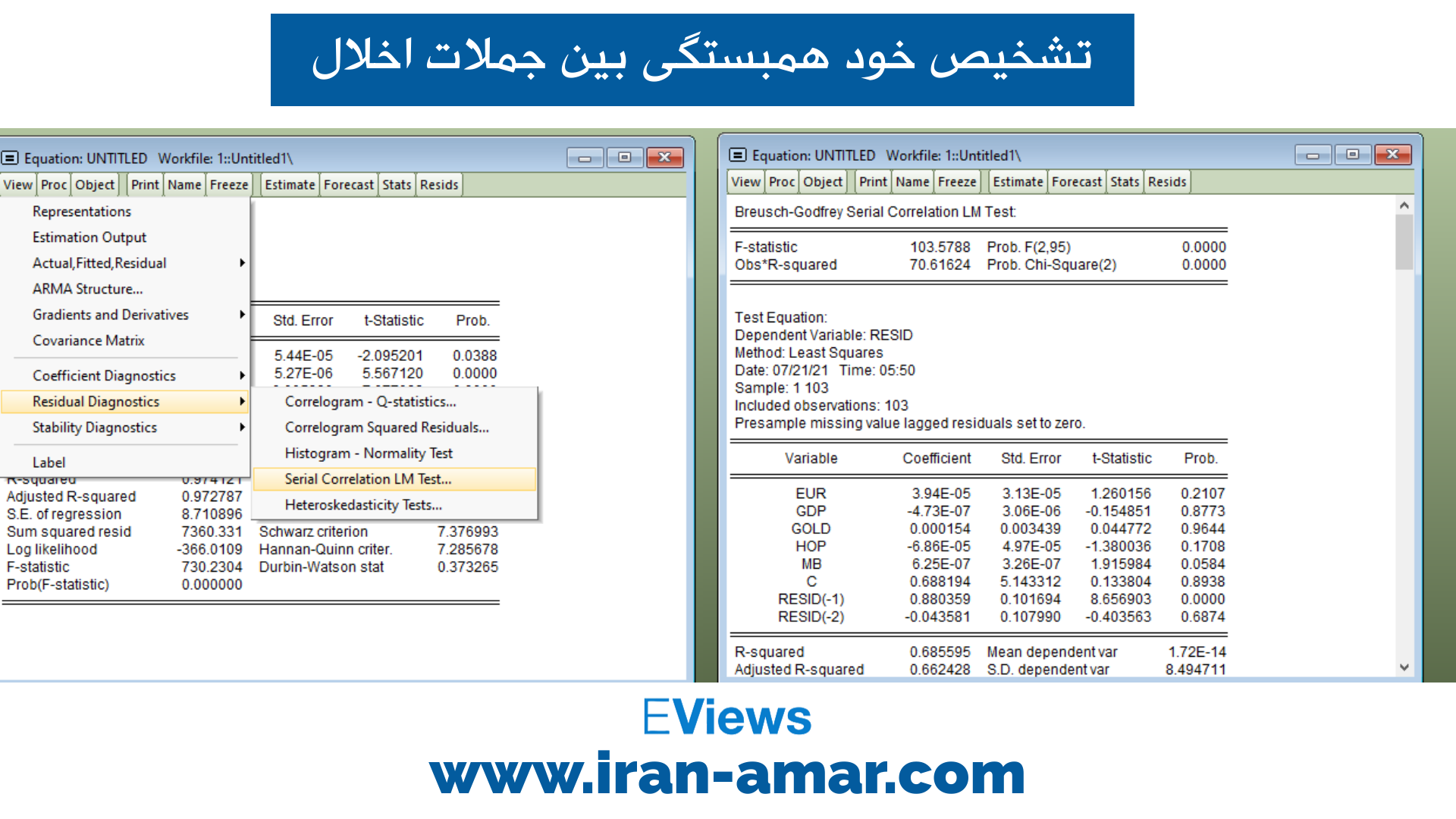
آزمون بعدی برای تشخیص عدم خود همبستگی جملات اخلال آزمون براش -گادفری است. به این منظور در نرم افزار ایویوز بعد از برآورد مدل در خروجی از مسیر View/Residual Diagnostics/Serial Corroelation LM Test صفحه‌ی آزمون براش گادفری نمایان شده و  اگر احتمال مقدار آماره‌ی آزمون از 0.05 کم‌تر باشد مدل دچار خود‌همبستگی بین مقادیر باقی‌‍مانده است.

آزمون دوربین-واتسون (Durbin-Watson Test)

این آزمون به‌طور خاص برای بررسی خودهمبستگی خطاها در مدل‌های رگرسیونی طراحی شده است. آماره دوربین-واتسون (DW) با استفاده از خطاهای تخمینی محاسبه می‌شود و مقدار آن بین 0 تا 4 متغیر است. مقدار نزدیک به 2 نشان‌دهنده عدم خودهمبستگی است. مقادیر نزدیک به 0 یا 4 نشان‌دهنده وجود خودهمبستگی مثبت یا منفی هستند. آزمون دوربین-واتسون معمولاً برای داده‌های سری زمانی و به‌ویژه زمانی که تنها یک متغیر مستقل وجود دارد، بهتر عمل می‌کند. همچنین، این آزمون نمی‌تواند خودهمبستگی از درجه دوم و بالاتر را بررسی کند.

آزمون براش-گادفری (Breusch-Godfrey Test)

این آزمون به بررسی خودهمبستگی در مدل‌های رگرسیونی با بیش از یک متغیر مستقل پرداخته و می‌تواند خودهمبستگی از درجه دوم و بالاتر را نیز بررسی کند. در این آزمون، ابتدا مدل رگرسیونی را تخمین زده و سپس از خطاهای محاسبه شده برای آزمون خودهمبستگی استفاده می‌شود. آماره تست معمولاً از توزیع خی‌دو (chi-squared) استفاده می‌کند. آزمون براش-گادفری انعطاف‌پذیری بیشتری دارد و می‌تواند برای مدل‌هایی با متغیرهای مستقل متعدد و خودهمبستگی‌های بالاتر از درجه اول کاربرد داشته باشد.

رفع خودهمبستگی فروض کلاسیک در ایویوز

رفع خودهمبستگی در مدل‌های رگرسیونی یکی از چالش‌های مهم در تحلیل‌های آماری است. وجود خودهمبستگی می‌تواند منجر به تخمین‌های نادرست از ضرایب و ارزیابی‌های غیرمعتبر شود.

• یکی از روش‌های اصلی برای کاهش خودهمبستگی، اضافه کردن متغیرهای تأخیری به مدل است. با استفاده از مقادیر گذشته متغیر وابسته یا مستقل، می‌توان خودهمبستگی را کنترل کرد.
• مدل‌های خودرگرسیو و میانگین متحرک (ARIMA) به‌طور خاص برای داده‌های سری زمانی طراحی شده‌اند و می‌توانند خودهمبستگی را به خوبی مدیریت کنند. این مدل‌ها می‌توانند به تحلیل دقیق‌تری از ساختار زمانی داده‌ها کمک کنند.
• تبدیل داده‌ها، مانند استفاده از تفاوت‌ها (differencing) یا لگاریتم‌ها، می‌تواند به رفع خودهمبستگی کمک کند. این روش‌ها می‌توانند تغییرات ناگهانی را که ممکن است منجر به خودهمبستگی شوند، کاهش دهند.
• استفاده از روش‌های تخمین مانند GEE (Generalized Estimating Equations) یا HAC (Heteroskedasticity and Autocorrelation Consistent) می‌تواند برای تخمین پارامترهای مدل بدون فرضیات نادرست درباره خودهمبستگی و ناهمسانی واریانس مفید باشد.
• گاهی اوقات، بررسی داده‌ها و شناسایی نقاط خارج از الگو (outliers) یا نادرستی‌ها در داده‌ها می‌تواند به کاهش خودهمبستگی کمک کند. حذف یا اصلاح این نقاط می‌تواند باعث بهبود مدل شود.

نرمال بودن توزیع جملات خطاها فروض کلاسیک در ایویوز

در صورتی که تعداد داده‌ها بیش از 30 باشد و فرض‌های قبلی برقرار باشند این اختلال نتایج را تحت تاثیر نمی‌گذارد. برای بررسی نرمال بودن جملات خطا پوشه‌ی با باز کردن پوشه‌ی سری resid01 و انتخاب گزینه‌ی  View/Descriptive Statistics & Tests/Histogram and Stats و پنجره‌ی زیر در نرم افزار ایویوز نمایش داده خواهد شد.

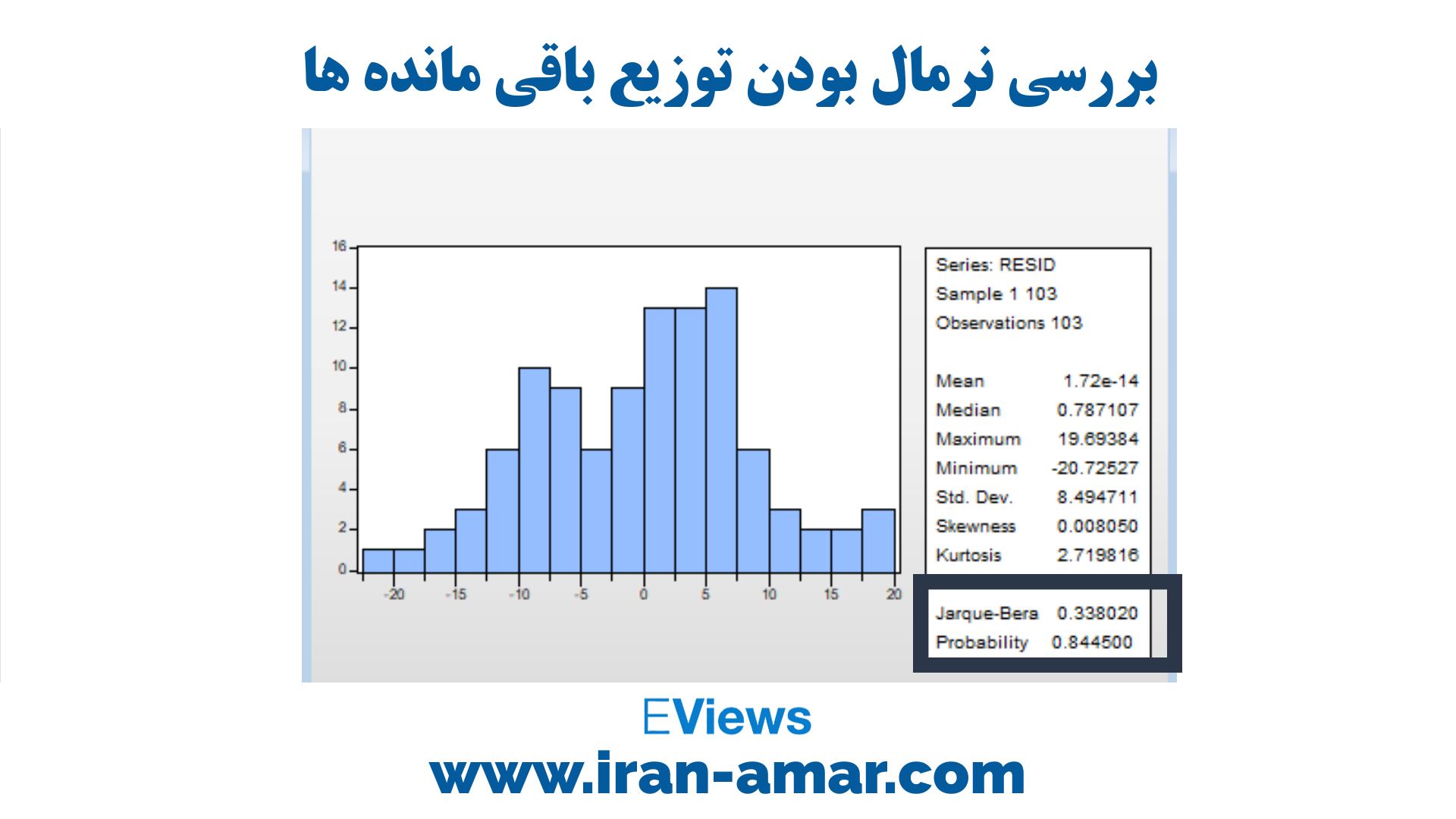
با توجه به مقدار آماره‌ی آزمون جارک-برا و احتمال آن در صورتی که Prob زیر 0.05 باشد توزیع باقی مانده‌ها نرمال نیست. در سطر اول میانگین جملات خطا نمایش داده شده است، ولی در این مدل مشاهده شده است که مقدار احتمال آزمون جارک‌برا برابر عدد 0.84 بوده و توزیع باقی‌مانده‌ها نرمال است.

رفع نرمال نبودن توزیع جملات خطاها فروض کلاسیک در ایویوز

در صورتی که توزیع باقی‌مانده‌ها نرمال نباشد می‌توان داده‌ها پرت را حذف کرد و دوباره مدل را برآورد کرد.

با لینک زیر می‌توانید به صفحه‌ی آموزش نرم افزار ایویوز  EViews ارائه شده به صورت رایگان، جامع و گام به گام  توسط گروه داده پردازی ایران آمار بروید.