EViews
سری زمانی واریانس ناهمسان
سری زمانی واریانس ناهمسان
در آموزش قبلی با سری زمانی واریانس همسان آشنا شدیم،در این آموزش با انواع فرآیندهای سری زمانی واریانس ناهمسان مانند فرآیند سری زمانی GARCH گارچ و ARCH آرچ آشنا و این سری زمانی ها را در نرم افزار ایویوز EViews بررسی می کنیم.
در داده های سری زمانی واریانس ناهم سان مانند داده های اقتصادی و بازار سرمایه فرض همسانی واریانس معمولا تایید نمی شود.
معمولا با ناهمسانی واریانس خوشه ای روبرو هستیم.برای این دسته از سری های زمانی نمی توان از تکنیک ARIMA استفاده کرد.
از فرآیند های سری زمانی با فرض ناهمسانی واریانس می توان انواع زیر را نام برد:
1-فرآیند خودتوضیح ناهمسانی واریانس شرطی مرتبه ی q؛(ARCH آرچ)
2-فرآیند خودتوضیح ناهمسانی واریانس شرطی تعمیم یافته مرتبه ی p؛ (GARCH گارچ)
3-فرآیند خودتوضیح ناهمسانی واریانس شرطی تعمیم یافته مرتبه ی (q,p)؛(GARCH(q,p))
1-فرآیند سری زمانی واریانس ناهمسان خود توضیح شرطی مرتبه ی q؛(ARCH آرچ)
سری های زمانی ای که مربع جملات خطا(باقی مانده ها) بتوانند واریانس خطا را توضیح دهند الگوی سری زمانی ARCH است.
فرض مهم مانایی متغیر های مستقل و وابسته و جمله ی خطا است.
به معادله زیر دقت کنید:
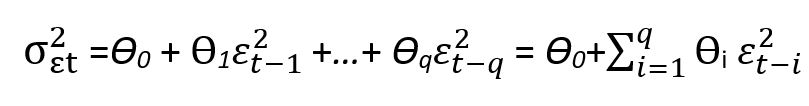
معادله ی بالا با نام معادله ی واریانس شرطی (Conditional variance equation) معروف است.
در این معادله ی واریانس سری زمانی ARCH نشان داده شده است که واریانس جملات اخلال در زمان t را می توان با مربع جملات خطا q دوره از دوره ی t تا t-q توضیح داد.
2-فرآیند خودتوضیح ناهمسانی واریانس شرطی تعمیم یافته مرتبه ی p؛(GARCH گارچ)
سری های زمانی ای که واریانس جملات خطا(باقی مانده ها) بتوانند واریانس خطا را توضیح دهند الگوی سری زمانی GARCH است.
به معادله زیر دقت کنید:
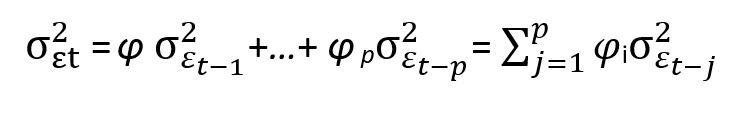
معادله ی بالا با نام معادله ی واریانس شرطی (Conditional variance equation) معروف است.
در این معادله ی واریانس سری زمانی GARCH نشان داده شده است که واریانس جملات اخلال در زمان t را می توان با مربع واریانس جملات خطا p دوره از دوره ی t تا t-p توضیح داد.
3-فرآیند خودتوضیح سری زمانی واریانس ناهمسان شرطی تعمیم یافته مرتبه ی (q,p)؛(GARCH(q,p))
سری زمانی GARCH(p,q) گارچ است که سری های زمانی واریانس جملات خطا(باقی مانده ها) و مربع جملات خطا(باقی مانده ها) بتوانند واریانس جملات خطای t دوره را توضیح دهند.
به معادله زیر دقت کنید:
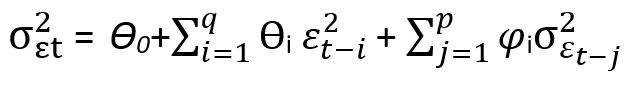
معادله ی بالا با نام معادله ی واریانس شرطی (Conditional variance equation) معروف است.
در این معادله ی واریانس سری زمانی GARCH(p,q) نشان داده شده است که واریانس جملات اخلال در زمان t را می توان با واریانس جملات خطا(باقی مانده ها)تعداد p دوره قبلی و مربع جملات خطا(باقی مانده ها) تعداد q دوره قبلی توضیح داد.
الگوی ARCH(q) معادل GARCH(q,0) و الگوی GARCH(p) معادل GARCH(0,p) است.
مدل سازی سری های زمانی ARCH و GARCH در نرم افزار ایویوز EViews
اولین قدم برای مدل سازی سری های زمانی با رویکرد ARCH و GARCH ابتدا مانایی سری زمانی را بررسی می کنیم.
در صورت مانا نبودن در سطح از سری زمانی تا جایی تفاضل گیری می کنیم که به یک سری مانا برسیم.
قدم بعدی بررسی همسانی واریانس است.
در صورتی که سری زمانی دارای مشکل ناهمسانی واریانس باشد،مدل سازی با رویکرد ARCH و GARCH انجام می گیرد.
قدم بعدی تعیین مرتبه ی (وقفه) بهینه به کمک معیار های آکایئک و شوارتز است.
در آخر برآورد مدل سری زمانی به روش ARCH یا GARCH انجام می گیرد.
بررسی وجود اثرات ARCH در نرم افزار ایویوز EViews
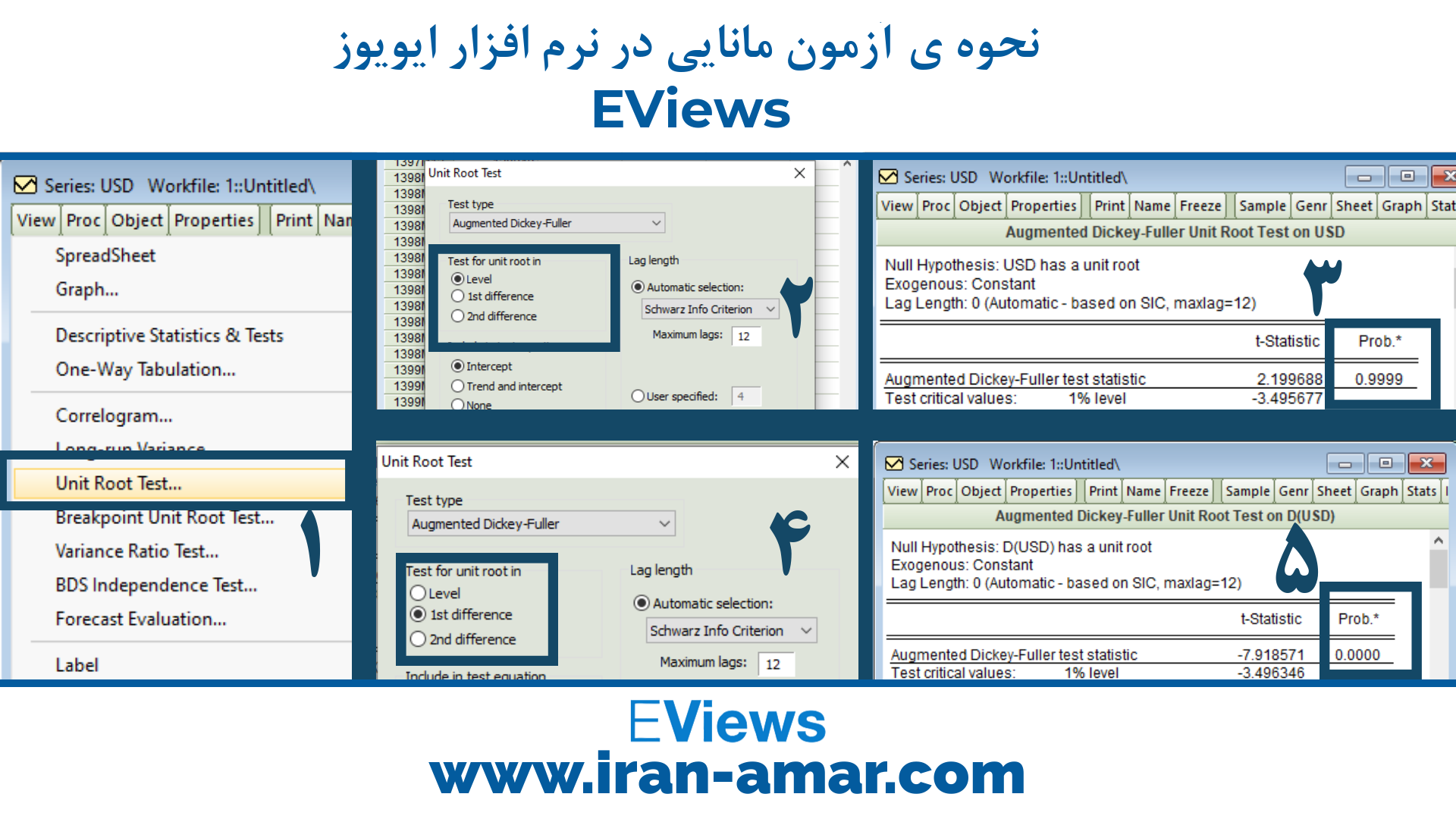
سری زمانی قیمت دلار را از سال 1391 تا سال 1399 به صورت ماهانه در نظر گرفته و آزمون مانایی را برای این سری بررسی می کنیم.
با توجه به تصویر مشاهده می شود که سری زمانی مد نظر در سطح نامانا است.
با یک بار تفاضل گیری،سری زمانی مانا شده است.
سری زمانی از نوع I(1) بوده با یک بار تفاضل گیری مانا شده است.
در مرحله ی بعد:
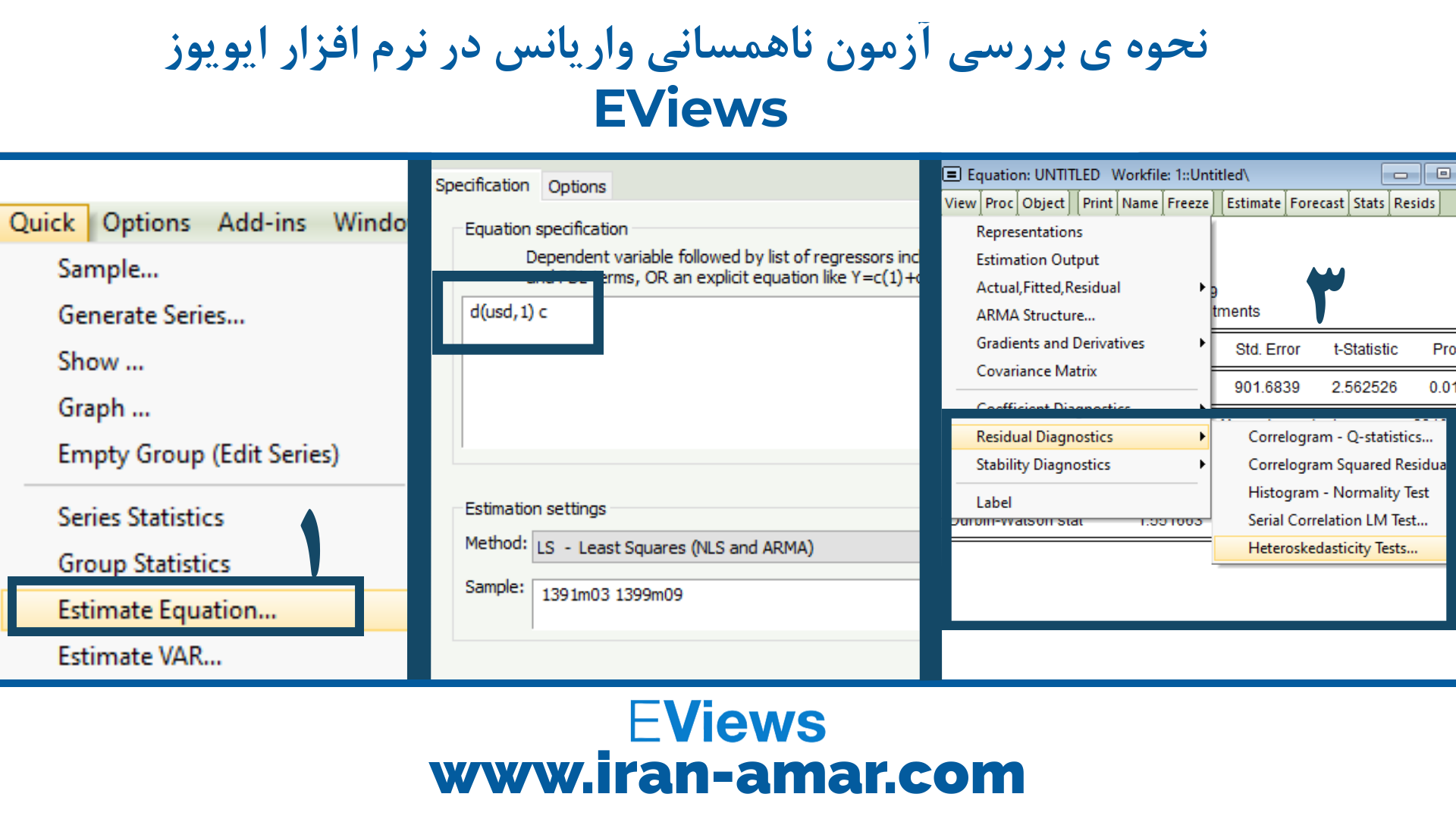
به سراغ برآورد سری زمانی با عرض از مبدا می رویم و ناهمسانی آن را آزمون می کنیم.
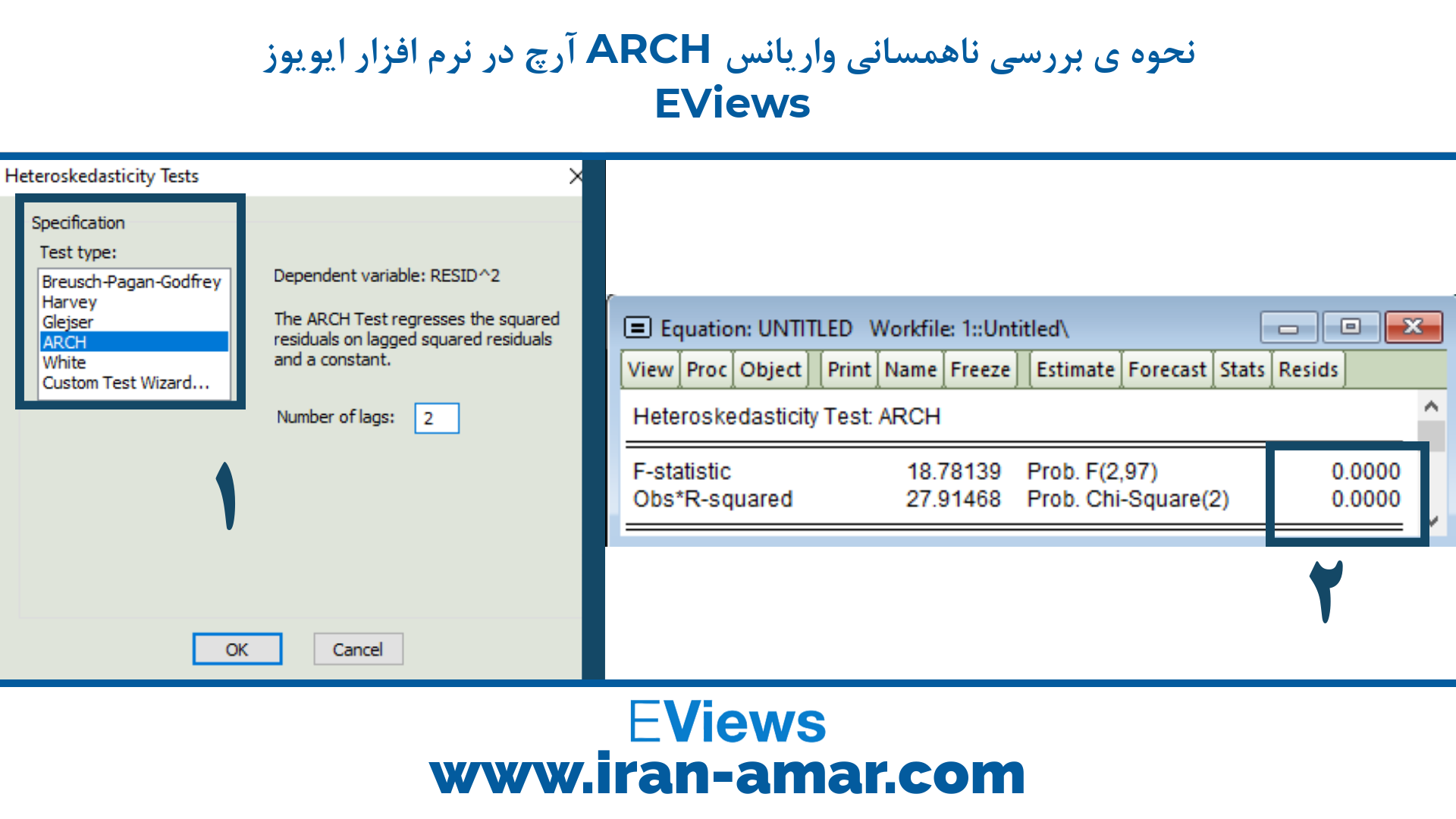
با روند مانند تصویر بالا و انتخاب ARCH در Test Type نتیجه آزمون ظاهر می شود.
و با توجه به مقدار Prob که کم تر از 0.05 است نتیجه می گیریم که جمله ی خطای معادله ی میانگین دارای مشکل ناهمسانی واریانس شرطی است.
با لینک زیر می توانید به صفحه ی آموزش نرم افزار ایویوز رایگان،جامع و گام به گام EViews بروید.
آموزش نرم افزار ایویوزاز طریق آیکون زیر برای تماس مستقیم تلفنی به منظور سفارش تحلیل و مشاوره با امور پشتیبانی اقدام نمایید.
واقعا دقیق و قوی و حرفه ای و به معنای واقعی کلمه میشه گفت عالی از هرلحاظ
با سلام
آزمون McLeod.li در ایویوز چطوری انجام میشه بهم کمک کنین ممنون میشم.
سلام در خط فرمان (Command) کد زیر را تایپ کنید
McLeod.Li.test(y=data)
به جای دیتا سری زمانی پژوهش را بذارید.
مقاله زیر را هم مطالعه کنید
https://core.ac.uk/download/pdf/31144416.pdf
سلام در رابطه با تفسیر ARCH &GHARCH چه چیزی باید نوشته شود یا معنی شود ….سپاس گذارم اگر راهنمایی بفرمایید
سلام در مدل های گارچ و آرچ که به خاطر وجود ناهمسانی واریانس خوشه ای از این خانواده استفاده میکنیم ابتدا باید وجود اثرات ارچ آزمون بشود و بعد از پیدا کردن مدل مناسب از وقفه های ارچ یا گارچ، معادله میانگین و معادله واریانس را از نتایج خروجی مدل می توان گزارش کرد.