A title

Image Box text

مانایی

در این آموزش مفهوم مانایی و یا پایایی، ایستایی را بررسی و با مفهوم رگرسیون کاذب آشنا شده و نحوه‌ی گرفتن آزمون ریشه واحد، آزمون دیکی فولر تعمیم یافته (ADF)، آزمون unit root test ، آزمون فیلیپس پرون (PP) و تعیین درجه انباشتگی در نرم افزار ایویوز EViews بررسی کرده‌ایم.

برای درک کامل و دقیق‌تر مفاهیم مانایی، قبل از شروع این آموزش پیشنهاد می‌کنیم، مفاهیم انواع داده‌ها در اقتصاد، داده‌های سری زمانی، نحوه‌ی جمع‌آوری داده‌های مالی و اقتصادی و نحوه‌ی وارد کردن داده‌ها در ایویوز  که قبلا توسط گروه داده پردازی ایران در همین وبسایت آموزش داده شده‌اند را مطالعه نمایید.

تعاریفی برای سری‌زمانی پایا مانا یا ایستا

مفاهیم مانایی، پایایی و ایستایی سری‌زمانی یک مفهوم دارند و هر سه در زبان لاتین معادل لغت Stationary هستند.

تمام تعاریف زیر مفهوم پایایی را بیان می‌کنند:

• سری زمانی‌ای که ریشه‌ی واحد ندارد.
• فرآیندی که توزیع مقادیر آن در طول زمان ثابت است.
• متغیری که شوک وارد شده زمانی را در خود حل کند.
• متغیری که اثرات شوک را در طول زمان از بین ببرد.
• در صورتی که طول دوره زمانی به سمت بی‌نهایت فرض شده باشد، گشتاورهای نمونه به سمت مقادیر جامعه میل کند.
• در سری پایا میانگین و واریانس متغیرها در طول زمان و کوواریانس متغیرها بین سال‌هاي مختلف ثابت بوده است .
• داده‌هایی مانا هستند که در طول زمان میانگین، واریانس و خودکواریانس‌شان در طول وقفه‌های یکسان با هم برابرند.

اگر به مرور به زمان گذشته برویم، اندازه‌ی ضرایب فرآیند خودتوضیح (آموزش فرآیند های سری زمانی) کم‌تر شود، بدین معناست که جملات قدیمی تاثیر کم‌تری در توضیح تغییرات متغیر وابسته دارند. تایید پایایی یک فرآیند تصادفی اجازه‌ی انجام فرض‌های آماری را صادر می‌کند و به عنوان اولین آزمون برای سری‌های زمانی باید بررسی شود. مفهوم ایستایی سري‌هاي زمانی در انتخاب مدل آماري تاثیر زیادي دارد.

به عنوان مثال اگر تمام متغیرها مانا باشند می‌توان از رگرسیون حداقل مربعات استفاده کرد. در متغیرهای سری زمانی، مانایی به عنوان یکی از ویژگی‌های مهم مورد در انجام مدل رگرسیونی است. مانایی به معنای پایداری و قابل اعتماد بودن سری‌زمانی است. زمانی که یک سری زمانی مانا است، الگوها، روندها و ویژگی‌های آماری در طول زمان تغییر کمی دارند و می‌توان به نتایج رگرسیون اعتماد کرد.

جهت ثبت سفارش و آگاهی از نحوه‌ی انجام پژوهش از یکی از صفحات زیر اقدام نمایید

یا

با شماره 09198278223 ارتباط برقرار کنید

جمع آوری داده

انجام فصل چهار پایان نامه

سفارش پایان نامه

رگرسیون کاذب چیست؟ نامانایی

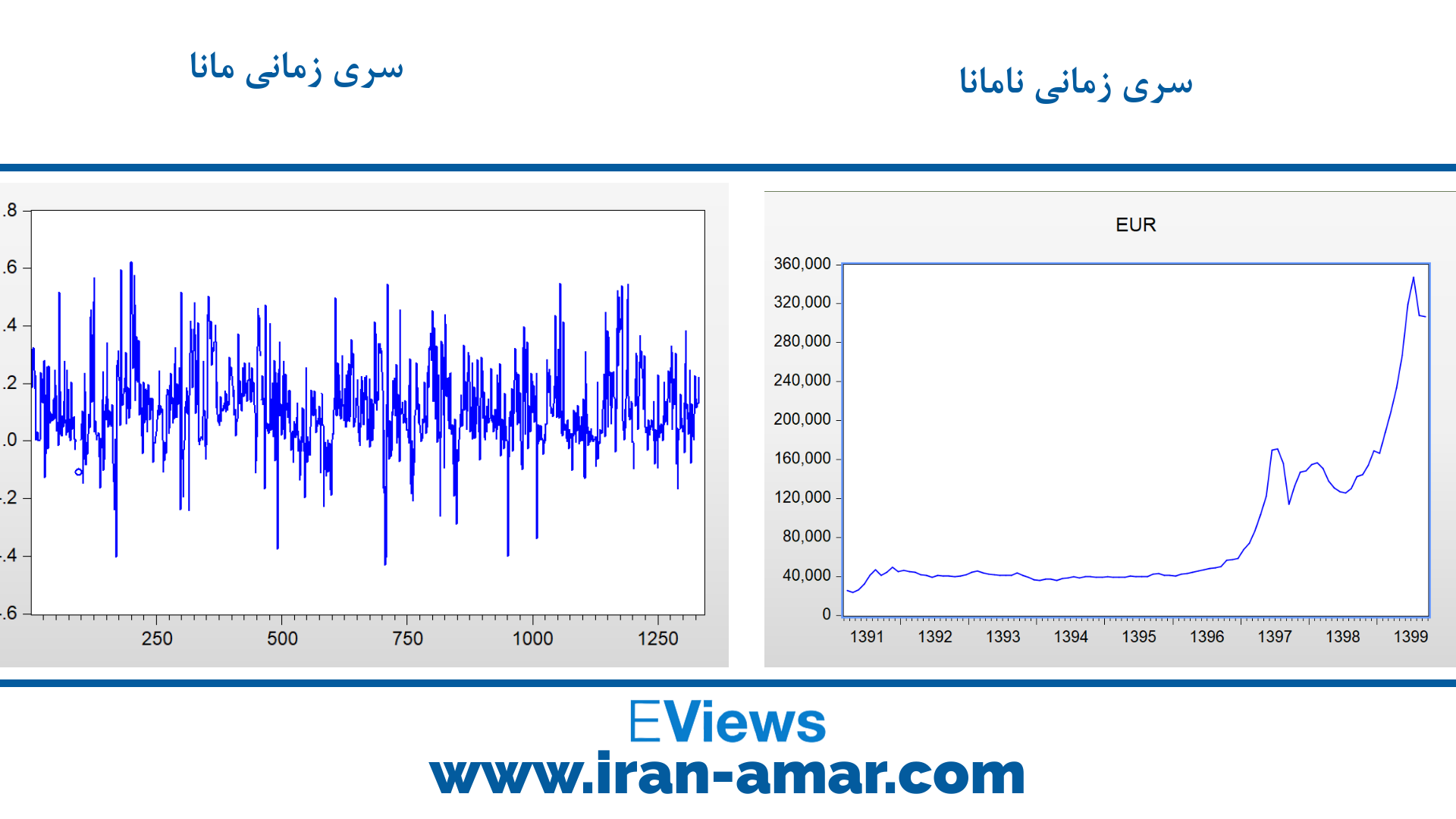
اگر سری زمانی‌ای قرار گرفته در مدل ناپایا باشد، نتایج خروجی مدل (تحلیل خروجی مدل در ایویوز) با ضریب تعیین بالا و آماره‌ی دوربین واتسون پایین گزارش خواهد شد. در تصویر زیر سری زمانی ناپایا و پایا را به ترتیب آورده شده است. در سری زمانی نامانا جهش شدید در دو مقطع مشاهده شده است که با تایید آزمون‌های ریشه واحد می‌توان گفت که سری زمانی پایا نیست.

تعیین درجه انباشتگی سری‌زمانی (آزمون ریشه واحد)

در پژوهش‌های سری زمانی برای پایایی (ایستایی) مقدار احتمال آزمون ریشه واحد بررسی خواهد شد. در آزمون‌های ریشه واحد فرض صفر وجود ریشه واحد (نامانایی) و فرض مقابل پایایی است. اگر فرض آزمون رد شود سری دارای ریشه واحد است و مانا نیست.

برای تعیین ریشه واحد از آزمون‌های فیلیپس پرون (PP) و دیکی فولر تعمیم یافته (ADF) مورد استفاده قرار می‌گیرند. تفاوت این دو آزمون این است که آزمون فیلیپس پرون (PP) توانایی تشخیص شکست ساختاری را دارد اما آزمون دیکی فولر تعمیم یافته (ADF) توانایی تشخیص شکست ساختاری را ندارد.

انجام آزمون مانایی در نرم افزار ایویوز EViews

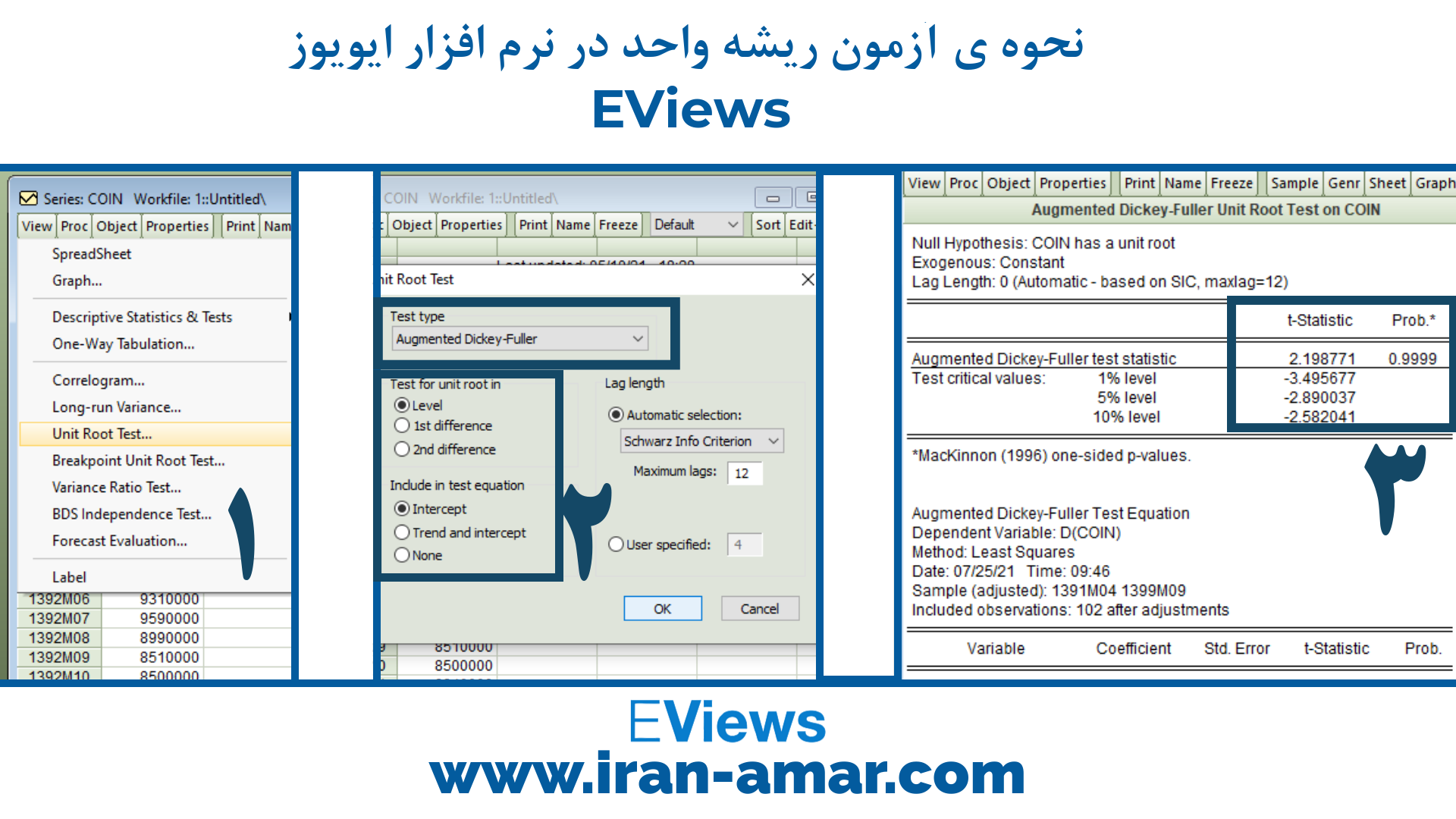
بعد از وارد کردن داده‌های سری زمانی (نحوه ی وارد کردن داده به نرم افزار ایویوز)، دو بار روی متغیر کلیک کرده تا مقادیر متغیر نشان داده شود. در ادامه  از  مسیر View/Unit Root Test در پنجره ی باز شده از قسمت Test Type در در نرم افزار ایویوز EViews یکی از دو آزمون دیکی فولر و یا فیلیپس پرون انتخاب شود.

در قسمت Test for unit root in سطح داده‌های مورد استفاده را ابتدا روی Level قرار داده و دکمه ok را می‌زنیم.

بررسی نتایج آزمون مانایی (ریشه واحد) در نرم افزار ایویوز EViews

در تصویر بالا و انجام مراحل یک تا سه، نرم‌افزار برای آزمون unit root test مقدار احتمال و آماره‌ی آزمون را خروجی داده است. اگر در پنجره‌ی باز شده مقدار Prob  کم تر از 0.05 بود، فرض صفر آزمون که ناپایایی است رد می‌شود و متغیر مانا است یا درجه انباشنگی متغیر صفر و از مرتبه ی I(0) است.

اما در عکس بالا متغیر سری‌زمانی  COIN آزمون شده و مقدار احتمال آزمون دیکی فولر (Prob)  عدد 0.9999  شده است پس آماره‌ی آزمون معنادار نیست و متغیر انباشته از درجه ی صفر نیست. به همین دلیل لازم است پایایی متغیر در تفاضل مرتبه‌ی اول بررسی شود.

اگر نمودار سری زمانی بدون عرض از مبدا و روند باشد در قسمت Test for unit root in سطح داده های مورد استفاده این بار روی 1st difference قرار داده می‌شود. نرم افزار ایویوز EViews یک بار از داده‌های سری زمانی تفاضل‌گیری می‌کند (در ادامه نحوه‌ی تفاضل گیری آموزش داده شده است) و مجددا ازمون را با داده‌های تفاضل‌گیری شده انجام می‌دهد.

آزمون مانایی (ریشه واحد) با تفاضل گیری در ایویوز EViews

با توجه به تصویر بالا، نرم‌افزار ایویوز برای آزمون unit root test با تفاضل مرتبه‌ی اول خروجی داده است. چنان‌چه در پنجره ی باز شده مقدار Prob  کم تر از 0.05 بود آماره‌ی آزمون معنادار و درجه‌ی انباشتگی  از مرتبه ی I(1) است.

در این سری زمانی آزمون شده مقدار Prob عدد 0.9237  است، در نتیجه آماره‌ی آزمون معنادار نیست و سری داده‌ها انباشته از درجه‌ی یک نیست.

به همین دلیل لازم است پایایی آن در تفاضل مرتبه ی دوم بررسی شود. اگر نمودار بدون عرض از مبدا و روند باشد در قسمت Test for unit root in سطح داده‌های مورد استفاده این بار روی 2nd difference قرار داده می‌شود.

با این کار نرم افزار ایویوز EViews دوباره از داده‌ها تفاضل‌گیری و مجددا ازمون را با داده‌های تفاضل‌گیری شده انجام می‌دهد.

آزمون ریشه واحد با تفاضل گیری مرتبه دوم در ایویوز EViews

با توجه به تصویر بالا و انجام مراحل یک تا سه، نرم‌افزار برای آزمون unit root test با دو بار تفاضل‌گیری خروجی داده‌ است. در پنجره‌ی باز شده نرم‌افزار در صورتی که مقدار Prob  کم تر از 0.05 باشد آماره‌ی آزمون معنادار و درجه‌ی انباشتگی سری از مرتبه ی I(2) است.

در سری آزمون شده مقدار Prob عدد 0.0001 است و آماره‌ی آزمون معنادار و در نتیجه سری زمانی انباشته از درجه‌ی دو است.

مراحل آزمون ریشه واحد آزمون فیلیپس پرون

ابتدا داده‌ها در سطح (Level) بدون هیچ‌گونه تفاضل‌گیری آزمون می‌شوند. اگر آماره‌ی آزمون معنادار بود (Prob کمتر از صفر)، انباشته از مرتبه ی I(0) است. در صورتی که فرض صفر آزمون رد نشد و متغیر در سطح نامانا بود، از داده‌ها یک بار تفاضل گرفته و آزمون دوباره انجام می‌شود.

در این مرحله اگر آزمون معنادار بود (Prob کمتر از صفر)، انباشته از مرتبه‌ی I(1) است. اگر فرض صفر رد نشد مجددا از متغیر تفاضل گرفته و این کار را P بار ادامه داده، تا سری مانا با مرتبه‌ی P حاصل شود. حال متغیر سری زمانی مانا با درجه انباشتگی P است.

تفاضل گیری برای پایایی

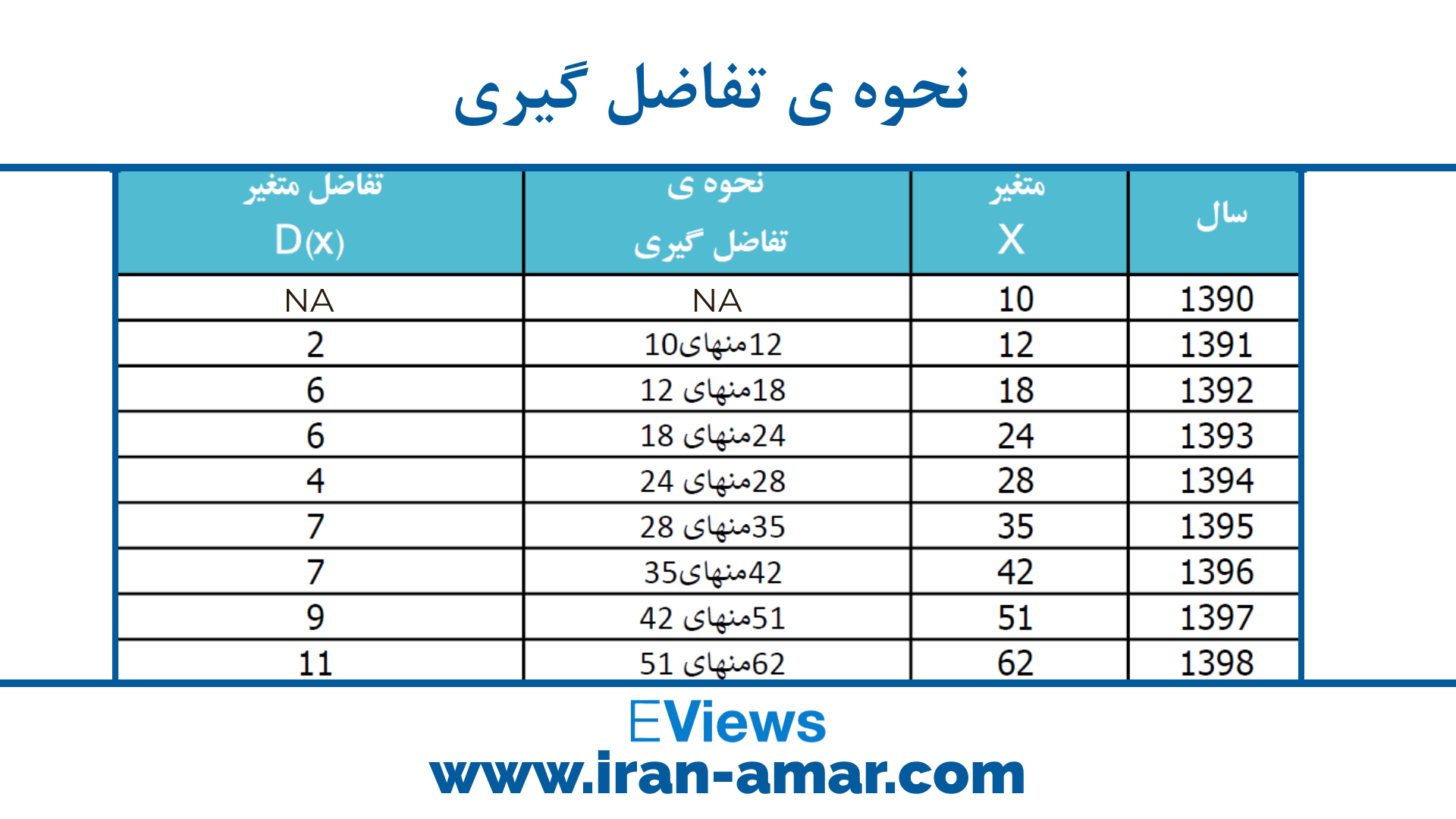
اگر سری زمانی با توجه به مقدار احتمال آزمون ریشه واحد نامانا بود برای برطرف کردن باید از تفاضل متغیر استفاده شود. مقدار دومین داده‌ی سری زمانی را از داده‌ی اول باید کم کرد. تا آخرین داده تفاضل‌گیری ادامه داده می‌شود.

در هر بار تفاضل گیری مقدار یک داده از سری زمانی را از دست می‌رود.

در تصویر زیر مقدار متغیر در سال 1390 و 1391 به ترتیب برابر 10 و 12 است. برای تفاضل گیری باید مقدار متغیر سال 1391 از مقدار متغیر در سال 1390 کم شود که نتیجه برابر با 2 خواهد شد. عدد 2 که حاصل تفاضل مقدار متغیر در سال 1390 و 1391 است حالا به مقدار متغیر در سال 1391 تبدیل شده است. این عمل را تا آخرین سال ادامه داده تا سری زمانی متغیر تفاضل کامل شود.

با لینک زیر می توانید به تمامی آموزش‌های ایویوز  رایگان، جامع و گام به گام  EViews بروید.

انجام پروژه نرم افزار ایویوز

جهت سفارش پروژه با نرم افزار ایویوز از طریق صفحه ی زیر با ما در ارتباط باشید