EViews
سری زمانی واریانس همسان
سری زمانی واریانس همسان:
سری زمانی واریانس همسان،در آموزش قبلی با مفهوم سری زمانی آشنا شدیم،در این آموزش با انواع فرآیندهای سری زمانی با فرض همسانی واریانس فرآیند خودتوضیح AR،میانگین متحرک MA،فرآیند خود توضیح میانگین متحرک ARMA و نحوه ی تعیین نوع فرآیند سری زمانی در نرم افزار ایویوز با استفاده از ریز برنامه ی ARIMASel آشنا می شویم.
فرآیند های سری زمانی با فرض هم سانی واریانس را می توان به سه دسته تقسیم کرد:
1- فرآیند خود توضیح (AR)
Autoregressive
2- فرآیند میانگین متحرک (MA)
Moving average
3- فرآیند خود توضیح میانگین متحرک (ARMA)
Autoregressive Moving average
1- فرآیند خودتوضیح (AR):سری زمانی واریانس همسان
سری زمانی واریانس همسان،اگر مقادیر پیشین داده های یک متغیر (وقفه)(Laged values)،بتوانند تغییرات داده های زمان حال را توضیح دهند به سری زمانی،فرآیند خودتوضیح می گویند.
فرمول فرآیند مدل خود توضیحی زیر را در نظر بگیرید:
همانطور که در فرمول بالا مشاهده می شود متغیر X در زمان t توسط زمان های گذشته ی خود متغیر تعریف شده می شود.
2- فرآیند میانگین متحرک (MA):سری زمانی واریانس همسان
اگر مقادیر پیشین جملات خطای مدل (وقفه)(Laged values)،بتوانند تغییرات داده های زمان حال را توضیح دهند به سری زمانی،فرآیند میانگین متحرک گفته خواهد شد.
فرمول فرآیند میانگین متحرک زیر را در نظر بگیرید:
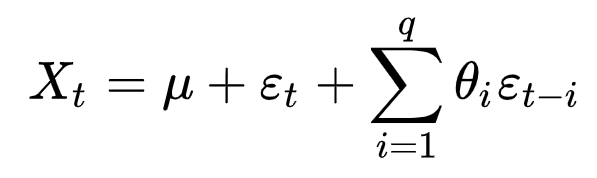
همانطور که در فرمول بالا مشاهده می شود متغیر X در زمان t توسط زمان های گذشته ی باقی مانده های متغیر ε تعریف شده است.
3-خود توضیح میانگین متحرک ARMA:
اگر مقادیر پیشین جملات خطای مدل (وقفه)(Laged values) و وقفه های جمله ی خطا،بتوانند تغییرات داده های زمان حال را توضیح دهند به سری زمانی،فرآیند میانگین متحرک می گویند.
فرمول فرآیند خود توضیح میانگین متحرک زیر را در نظر بگیرید:
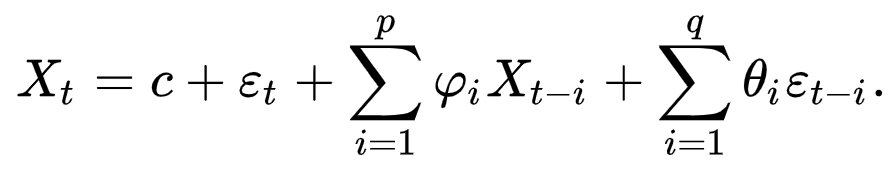
همانطور که در فرمول بالا مشاهده می شود متغیر X در زمان t توسط زمان های گذشته ی باقی مانده های متغیر ε و زمان های گذشته ی خود متغیر تعریف شده است.
تعیین نوع فرآیند سری زمانی در ایویوز EViews:
برای تعیین نوع فرآیند یک سری زمانی در ایویوز ساده ترین و دقیق ترین روش اجرای یک افزونه یا زیر برنامه ارائه شده توسط نرم افزار ایویوز EViews می باشد.
به منظور دانلود این پلاگین باید وارد سایت اصلی نرم افزار ایویوز شد و از تب
User Community/EViews Add-in
وارد صفحه ریز برنامه های ایویوز شد.
از مسیر لینک گذاشته شده در اینجا مستقیم به صفحه ریز برنامه ایویوز وارد شوید.
برای دانلود ریز برنامه ی ARIMASel با لینک مستقیم از اینجا اقدام کنید.
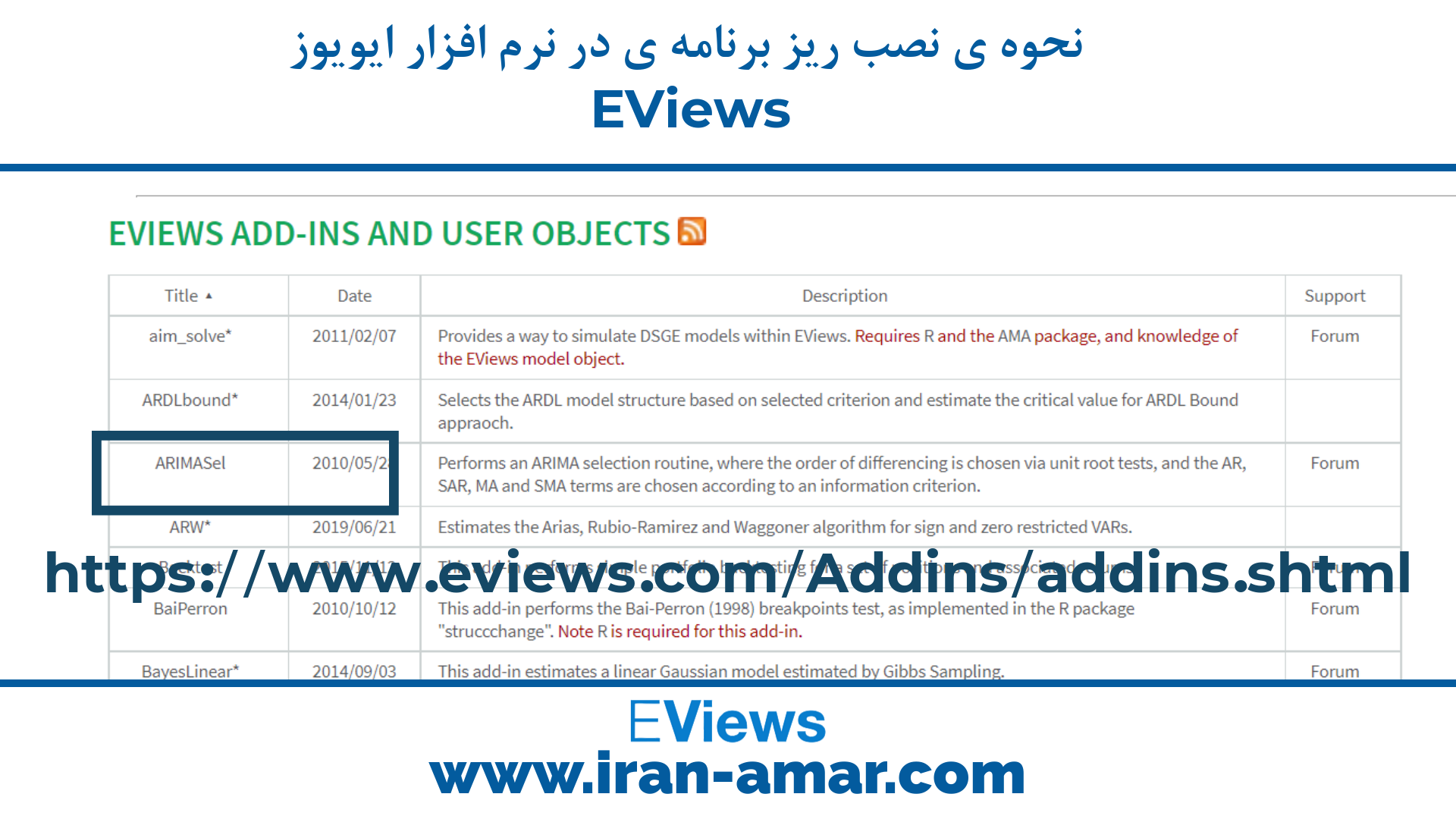
در جدولی مانند تصویر زیر از بخش Title ریز برنامه به نام ARIMASel را انتخاب کنید و مستقیم دانلود کنید.
بعد از دانلود در سیستم خود ریز برنامه را پیدا کنید و روی آن کلیک کنید.
ریز برنامه را نصب کنید.
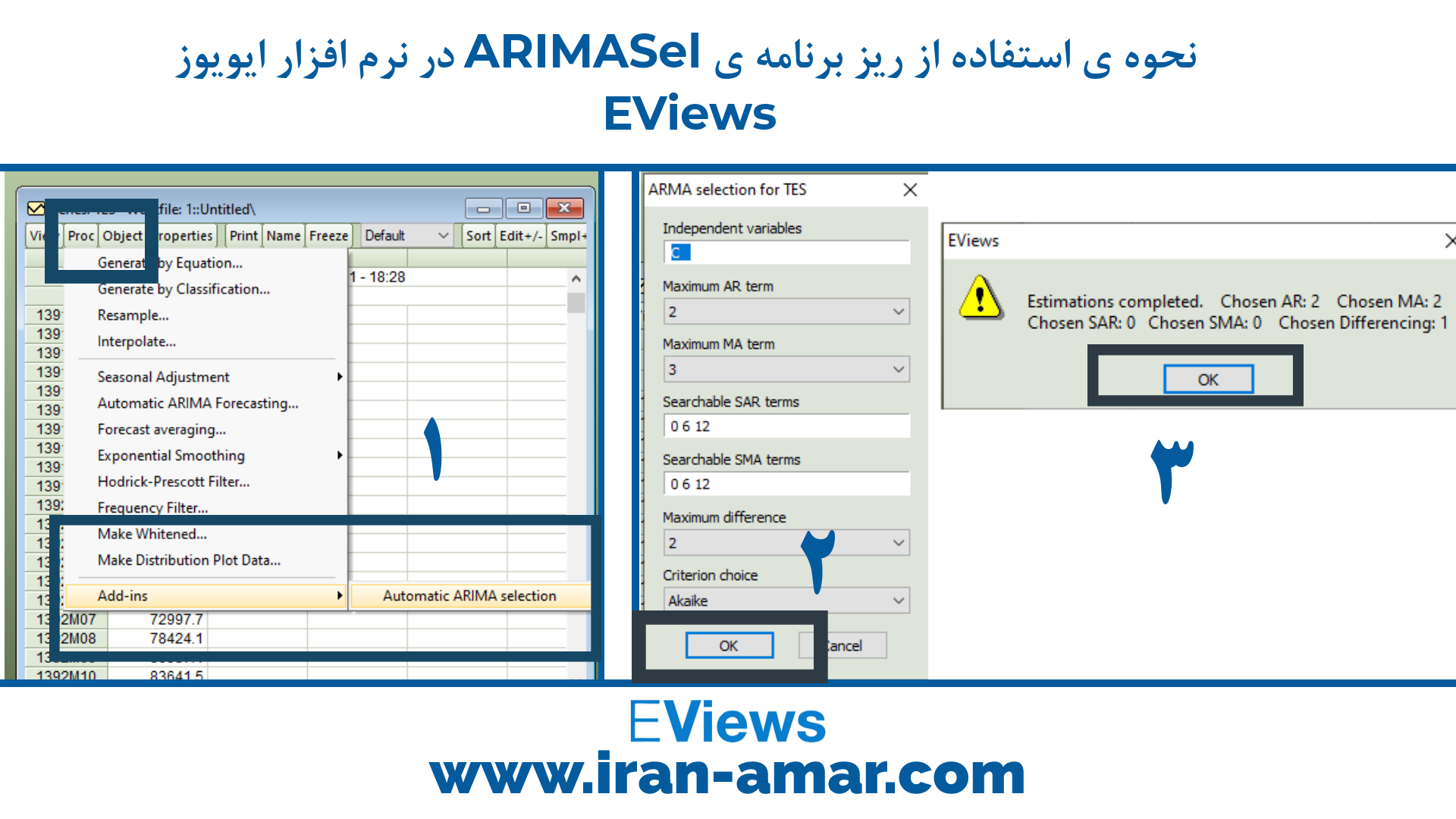
نحوه ی استفاده از ریز برنامه ی ARIMASel:
پوشه ی سری زمانی که می خواهید فرآیند آن را بررسی کنید باز کنید.
از مسیر
Proc/Add-ins/Automatic ARIMA selection
در پنجره ای که باز می شود بدون تغییر OK کنید.
در پنجره ی کوچکی که باز می شود پارامتر های بهترین ترکیب ارائه می شود.
ok را بزنید و مانند تصویر زیر دو جدول باز می شود:
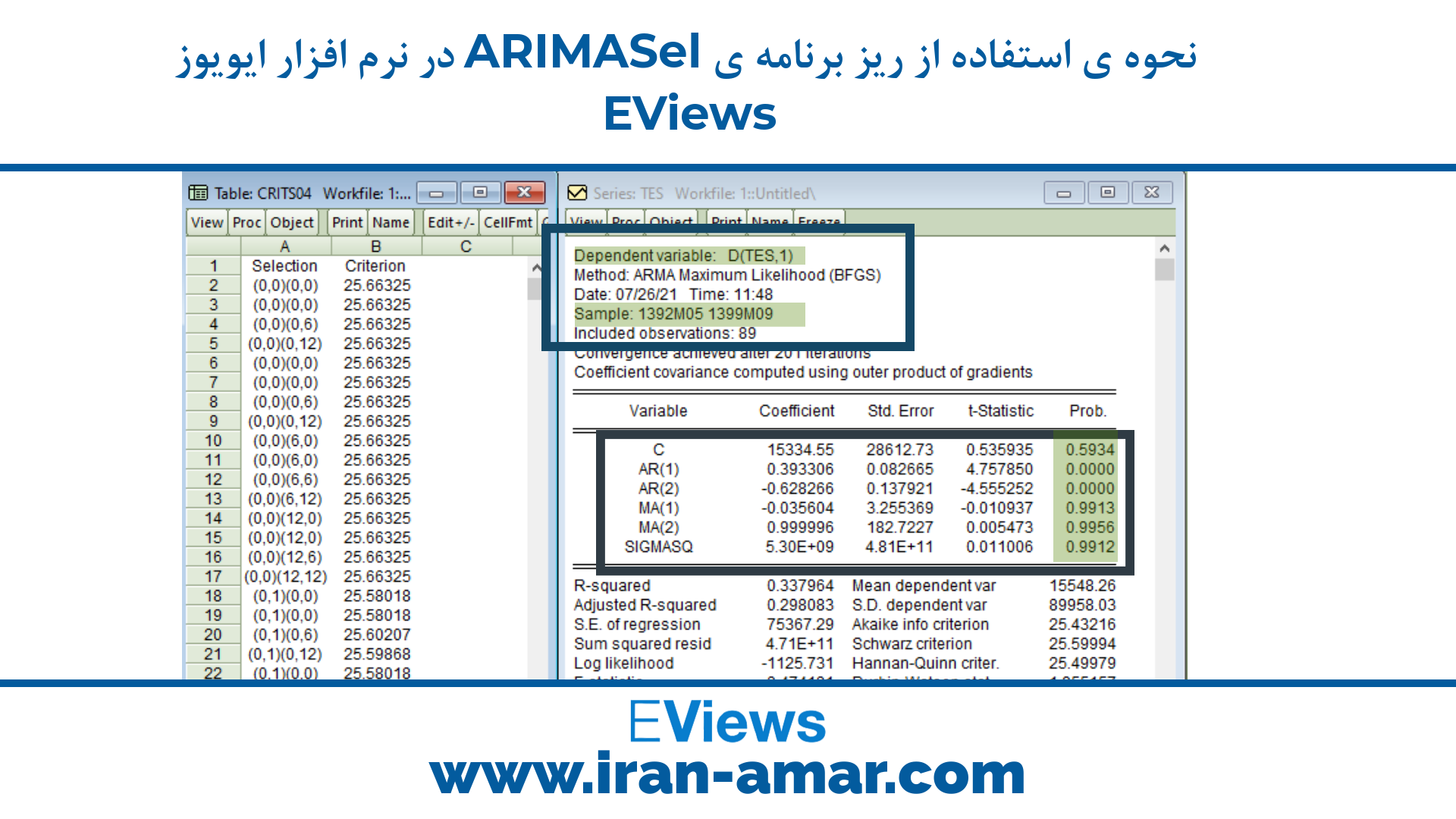
تحلیل خروجی زیر برنامه ی ARIMASel:
تصویر بالا خروجی انواع فرآیندهای سری زمانی را نمایش می دهد.
در تصویر بالا دو قسمت هایلایت شده است و مشخص است که یک بار از متغیر سری زمانی D(TSE,1) تفاضل گیری شده است.
بازه ی زمانی که متفاوت با بازه ی سری زمانی اصلی است و دلیل آن اعمال جملات خود توضیح است.
در جدول معناداری تصویر بالا مشاهده می شود که AR(1) و AR(2) معنادارند چون Prob آن ها زیر 0.05 است.
در نتیجه فرآیند این سری زمانی بعد از یکبار تفاضل گیری AR(2) است.
با لینک زیر می توانید به صفحه ی آموزش نرم افزار ایویوز رایگان،جامع و گام به گام EViews بروید.
آموزش نرم افزار ایویوزاز طریق آیکون زیر برای تماس مستقیم تلفنی به منظور سفارش تحلیل و مشاوره با امور پشتیبانی اقدام نمایید.

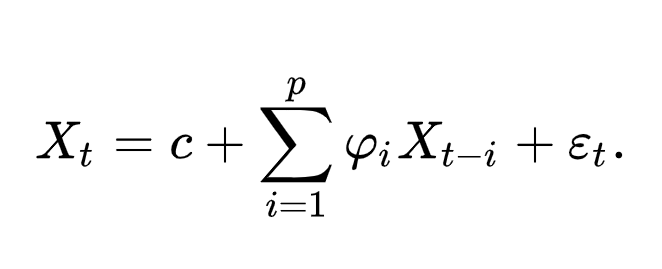
دقیق و خوب از همه لحاظ
کامل و خوب. من که راضی بودم…
ممنون از توجه تون